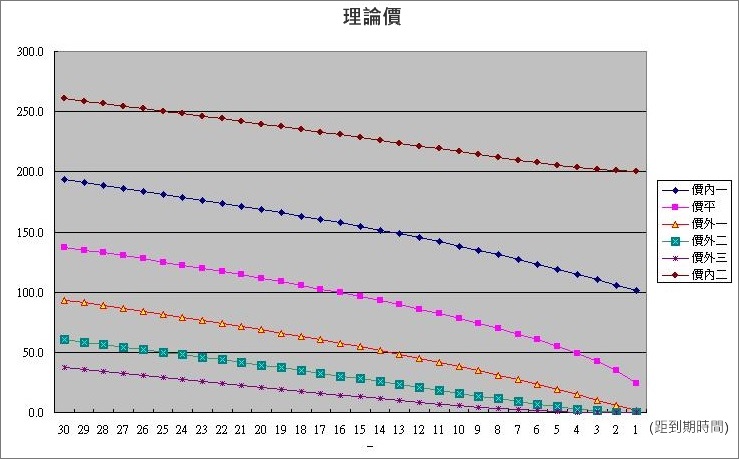
要進入選擇權的交易世界裡,先要知道影響權利金的因素有哪些,以及他如何影響權利金。以下的圖形都是由 B-S模型中推導出的,這裡不介紹數學模型用圖形表現大家比較容易看的懂。
- 假設指數與利率不變且波動率=20%
- 時間為唯一的變數
所以圖形所表現的就是從開倉日到最後交易日,權利金增減點數的變化。
各履約價的理論價會隨著希臘字母而變化
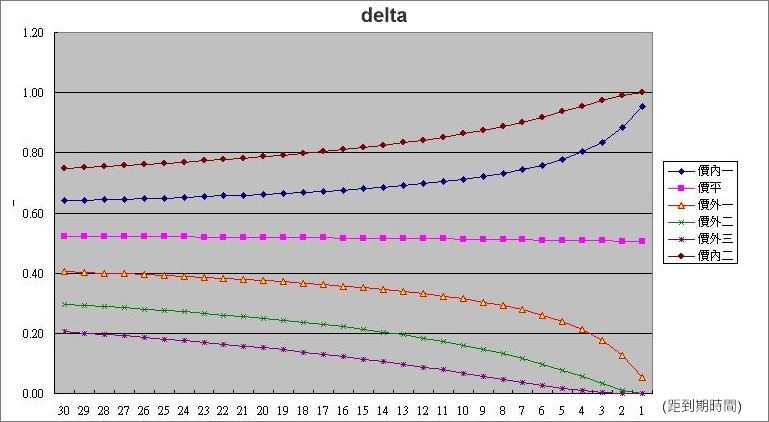
delta(δ) = ∂C/∂S
選擇權價格之一次微分,代表指數變動一點,對選擇權的價格貢獻度。
例:delta(δ) = 0.5
表示指數漲1點,權利金會漲0.5點
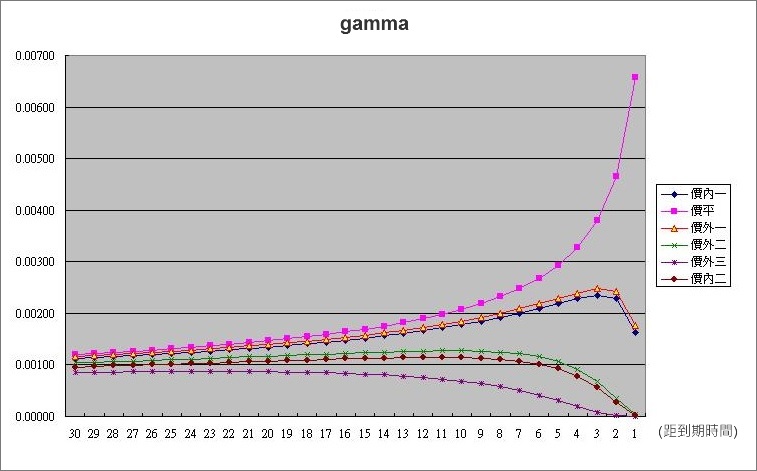
gamma(γ) = ∂(delta)/∂S
Gamma是對選擇權價格的二次微分,也就是震盪係數,其定義是指數變動一點時,Delta值會改變的數量,所以說Gamma值是用來衡量Delta值得安定程度,Gamma值越高表示Delat值越不穩定,反之越低表示Delta值越穩定。
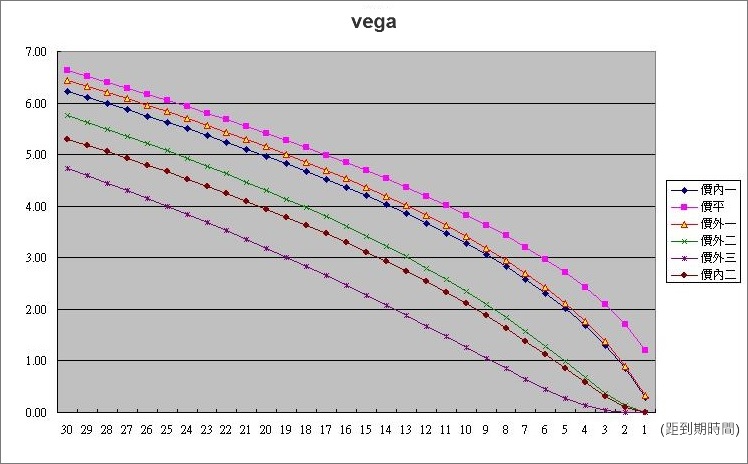
vega(ν) =∂C/∂σ
Vega是選擇權價格依隱含波動率變動進行之微分,其定義是若隱含波動率增加1%,選擇權價格會提高多少。
例:到期前第17天,價平Vega = 5
表示隱含波動率增加1%,權利金會漲5點
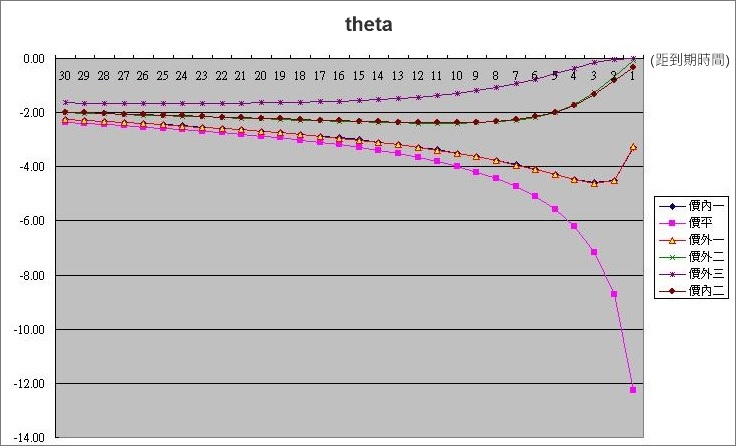
theta(θ) = ∂C/∂T
Theta是對選擇權價格依時間進行之微分,也就是時間每經過一天,選擇權價值會被吃掉多少。
例:到期前第10天,價平theta(θ) = -5
表示到期前第10天 ,權利金會跌5點